Introduction
The previous article considered the creation of a simple neuron (perceptron). We learned about gradient descent method, about the construction of the multilayer perceptron (MLP) network consisting of interconnected perceptrons and the training of such networks.
In this article, I want to demonstrate how easy it is to implement this algorithm type using the Python language.
There is a Python package available for developing integrations with MQL, which enables a plethora of opportunities such as data exploration, creation and use of machine learning models.
The built in Python integration in MQL5 enables the creation of various solutions, from simple linear regression to deep learning models. Since this language is designed for professional use, there are many libraries that can execute hard computation-related tasks.
We will create a network manually. But as I mentioned in the previous article, this is only a step which helps us understand what actually happens in the learning and prediction process. Then I will show a more complex example using TensorFlow and Keras.
What is TensorFlow?
TensorFlow is an open-source library for fast numerical processing.
It was created, supported and released by Google under Apache open-source license. The API is designed for the Python language, although it has access to the basic C++ API.
Unlike other numeric libraries designed for use in deep learning, such as Theano, TensorFlow is intended for use both in research and in production. For example, the machine-learning based search engine RankBrain used by Google and a very interesting computer vision project DeepDream.
It can run in small systems on one CPU, GPU or mobile devices, as well as on large-scale distributed systems which utilize hundreds of computers.
What is Keras?
Keras is a powerful and easy-to-use open-source Python library for developing and evaluating deep learning models.
It involves the powerful Theano and TensorFlow computation libraries. It allows the defining and training of neural network models in just a few lines of code.
Tutorial
This tutorial is divided into 4 sections:
- Installing and preparing the Python environment in MetaEditor.
- First steps and model reconstruction (perceptron and MLP).
- Creating a simple model using Keras and TensorFlow.
- How to integrate MQL5 and Python.
1. Installing and preparing the Python environment.
First, you should download Python from the official website www.python.org/downloads/
To work with TensorFlow, you should install a version between 3.3 and 3.8 (I personally use 3.7).
After downloading and starting the installation process, check the option “Add Python 3.7 to PATH”. This will ensure that some things will work without additional configuration later.
A Python script can then be easily run directly from the MetaTrader 5 terminal.
- Define the Python executable path (environment)
- Install required project dependencies
Open MetaEditor and go to Tools \ Options.
Specify here the path at which the Python executable is locates. Note that after installation it should have the default Python path. If not, enter the full path to the executable file manually. This will allow you to run scripts directly from your MetaTrader 5 terminal.
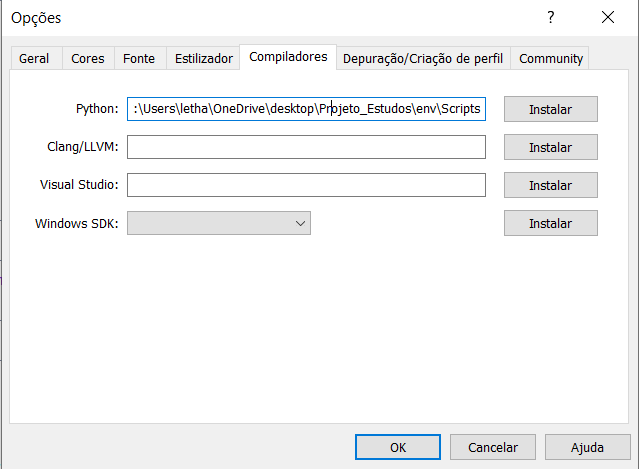
I personally use a completely separate library environment called virtual environment. This is a way to get “clean” installation and to collect only those libraries which are required for the product.
For more information about the venv package please read here.
Once done, you will be able to run Python scripts directly from the terminal. For this project, we need to install the following libraries.
If you are not sure about how to install the libraries, please see the relevant module installation guide.
- MetaTrader 5
- TensorFlow
- Matplotlib
- Pandas
- Learn
Now that we have installed and configured the environment, let’s conduct a small test to understand how to create and run a small script in the terminal. To start a new script directly from MetaEditor, follow the steps below:
New > Python Script
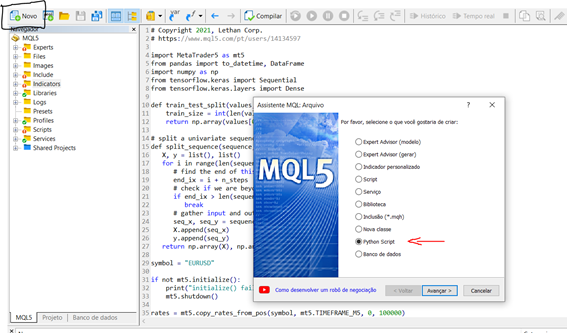
Specify the name for your script. The MQL Wizard in MetaEditor will automatically prompt you to import some libraries. It is very interesting, and for our experiment let’s select the numpy option.
Now, let’s create a simple script that generates a sinusoidal graph.
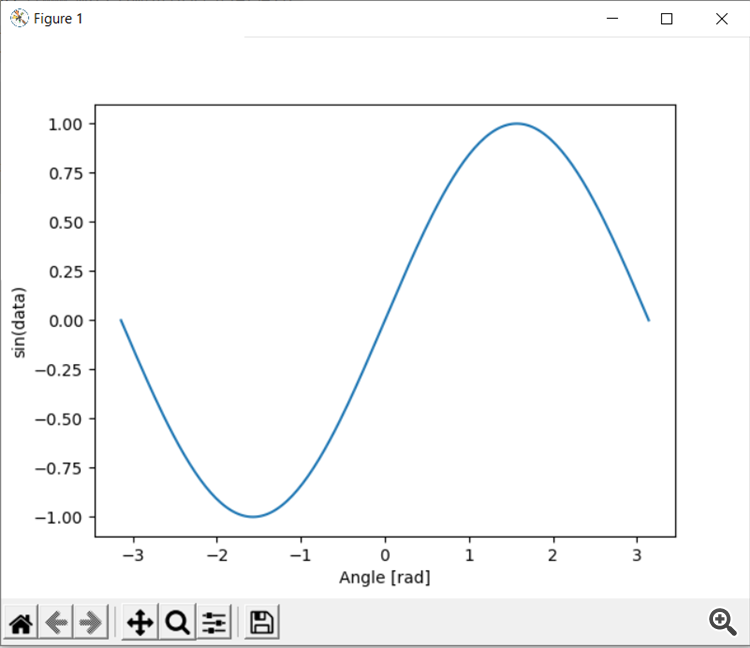
# Copyright 2021, Lethan Corp. # https://www.mql5.com/pt/users/14134597 import numpy as np import matplotlib.pyplot as plt data = np.linspace(-np.pi, np.pi, 201) plt.plot(data, np.sin(data)) plt.xlabel( 'Angle [rad]' ) plt.ylabel( 'sin(data)' ) plt.axis('tight') plt.show()
To run the script, simply press F7 to compile, open the MetaTrader 5 terminal and run the script on a chart. The results will be shown in the experts tab if it has something to print. In our case, the script will open a window with the function graph that we have created.
2. First steps and model reconstruction (perceptron and MLP).
For convenience, we will use the same dataset as in the MQL5 example.
Below is the predict() function which predicts the output value for a line with the given set of weights. Here the first case is also the bias. Also, there is an activation function.
# Transfer neuron activation def activation(activation): return 1.0 if activation >= 0.0 else 0.0 # Make a prediction with weights def predict(row, weights): z = weights[0] for i in range(len(row) - 1): z += weights[i + 1] * row[i] return activation(z)
As you already know, to train a network we need to implement the gradient descent process, which was explained in detail in the previous article. As a continuation, I will show the training function “train_weights()”.
# Estimate Perceptron weights using stochastic gradient descent def train_weights(train, l_rate, n_epoch): weights = [0.0 for i in range(len(train[0]))] #random.random() for epoch in range(n_epoch): sum_error = 0.0 for row in train: y = predict(row, weights) error = row[-1] - y sum_error += error**2 weights[0] = weights[0] + l_rate * error for i in range(len(row) - 1): weights[i + 1] = weights[i + 1] + l_rate * error * row[i] print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error)) return weights
Application of the MLP model:
This tutorial is divided into 5 sections:
- Network launch
- FeedForward
- BackPropagation
- Training
- Forecast
Network launch
Let’s start with something simple by creating a new network that is ready to learn.
Each neuron has a set of weights that need to be maintained, one weight for each input connection and an additional weight for bias. We will need to save additional properties of the neuron during training, therefore we will use a dictionary to represent each neuron and to store properties by names, for example as “weights” for weights.
from random import seed from random import random # Initialize a network def initialize_network(n_inputs, n_hidden, n_outputs): network = list() hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)] network.append(hidden_layer) output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)] network.append(output_layer) return network seed(1) network = initialize_network(2, 1, 2) for layer in network: print(layer)
Now that we know how to create and launch a network, let’s see how we can use it to calculate output data.
FeedForward
from math import exp # Calculate neuron activation for an input def activate(weights, inputs): activation = weights[-1] for i in range(len(weights)-1): activation += weights[i] * inputs[i] return activation # Transfer neuron activation def transfer(activation): return 1.0 / (1.0 + exp(-activation)) # Forward propagate input to a network output def forward_propagate(network, row): inputs = row for layer in network: new_inputs = [] for neuron in layer: activation = activate(neuron['weights'], inputs) neuron['output'] = transfer(activation) new_inputs.append(neuron['output']) inputs = new_inputs return inputs # test forward propagation network = [[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}], [{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]] row = [1, 0, None] output = forward_propagate(network, row) print(output)
By running the above script, we get the following result:
[0.6629970129852887, 0.7253160725279748]
The actual output values are absurd for now. But we’ll soon see how to make the weights in the neurons more useful.
Backpropagation
# Calculate the derivative of an neuron output def transfer_derivative(output): return output * (1.0 - output) # Backpropagate error and store in neurons def backward_propagate_error(network, expected): for i in reversed(range(len(network))): layer = network[i] errors = list() if i != len(network)-1: for j in range(len(layer)): error = 0.0 for neuron in network[i + 1]: error += (neuron['weights'][j] * neuron['delta']) errors.append(error) else: for j in range(len(layer)): neuron = layer[j] errors.append(expected[j] - neuron['output']) for j in range(len(layer)): neuron = layer[j] neuron['delta'] = errors[j] * transfer_derivative(neuron['output']) # test backpropagation of error network = [[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}], [{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095]}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763]}]] expected = [0, 1] backward_propagate_error(network, expected) for layer in network: print(layer)
When running, the example prints the network after completing error checks. As you can see, error values are calculated and saved in neurons for the output layer and the hidden layer.
[{‘output’: 0.7105668883115941, ‘weights’: [0.13436424411240122, 0.8474337369372327, 0.763774618976614], ‘delta’: -0.0005348048046610517}]
[{‘output’: 0.6213859615555266, ‘weights’: [0.2550690257394217, 0.49543508709194095], ‘delta’: -0.14619064683582808}, {‘output’: 0.6573693455986976, ‘weights’: [0.4494910647887381, 0.651592972722763], ‘delta’: 0.0771723774346327}]
Network training
from math import exp from random import seed from random import random # Initialize a network def initialize_network(n_inputs, n_hidden, n_outputs): network = list() hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)] network.append(hidden_layer) output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)] network.append(output_layer) return network # Calculate neuron activation for an input def activate(weights, inputs): activation = weights[-1] for i in range(len(weights)-1): activation += weights[i] * inputs[i] return activation # Transfer neuron activation def transfer(activation): return 1.0 / (1.0 + exp(-activation)) # Forward propagate input to a network output def forward_propagate(network, row): inputs = row for layer in network: new_inputs = [] for neuron in layer: activation = activate(neuron['weights'], inputs) neuron['output'] = transfer(activation) new_inputs.append(neuron['output']) inputs = new_inputs return inputs # Calculate the derivative of an neuron output def transfer_derivative(output): return output * (1.0 - output) # Backpropagate error and store in neurons def backward_propagate_error(network, expected): for i in reversed(range(len(network))): layer = network[i] errors = list() if i != len(network)-1: for j in range(len(layer)): error = 0.0 for neuron in network[i + 1]: error += (neuron['weights'][j] * neuron['delta']) errors.append(error) else: for j in range(len(layer)): neuron = layer[j] errors.append(expected[j] - neuron['output']) for j in range(len(layer)): neuron = layer[j] neuron['delta'] = errors[j] * transfer_derivative(neuron['output']) # Update network weights with error def update_weights(network, row, l_rate): for i in range(len(network)): inputs = row[:-1] if i != 0: inputs = [neuron['output'] for neuron in network[i - 1]] for neuron in network[i]: for j in range(len(inputs)): neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j] neuron['weights'][-1] += l_rate * neuron['delta'] # Train a network for a fixed number of epochs def train_network(network, train, l_rate, n_epoch, n_outputs): for epoch in range(n_epoch): sum_error = 0 for row in train: outputs = forward_propagate(network, row) expected = [0 for i in range(n_outputs)] expected[row[-1]] = 1 sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))]) backward_propagate_error(network, expected) update_weights(network, row, l_rate) print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error)) # Test training backprop algorithm seed(1) dataset = [[2.7810836,2.550537003,0], [1.465489372,2.362125076,0], [3.396561688,4.400293529,0], [1.38807019,1.850220317,0], [3.06407232,3.005305973,0], [7.627531214,2.759262235,1], [5.332441248,2.088626775,1], [6.922596716,1.77106367,1], [8.675418651,-0.242068655,1], [7.673756466,3.508563011,1]] n_inputs = len(dataset[0]) - 1 n_outputs = len(set([row[-1] for row in dataset])) network = initialize_network(n_inputs, 2, n_outputs) train_network(network, dataset, 0.5, 20, n_outputs) for layer in network: print(layer)
After training, the network is printed, showing the learned weights. Also, the network still has output and delta values which can be ignored. If necessary, we could update our training function to delete this data.
>epoch=13, lrate=0.500, error=1.953
>epoch=14, lrate=0.500, error=1.774
>epoch=15, lrate=0.500, error=1.614
>epoch=16, lrate=0.500, error=1.472
>epoch=17, lrate=0.500, error=1.346
>epoch=18, lrate=0.500, error=1.233
>epoch=19, lrate=0.500, error=1.132
[{‘weights’: [-1.4688375095432327, 1.850887325439514, 1.0858178629550297], ‘output’: 0.029980305604426185, ‘delta’: -0.0059546604162323625}, {‘weights’: [0.37711098142462157, -0.0625909894552989, 0.2765123702642716], ‘output’: 0.9456229000211323, ‘delta’: 0.0026279652850863837}]
[{‘weights’: [2.515394649397849, -0.3391927502445985, -0.9671565426390275], ‘output’: 0.23648794202357587, ‘delta’: -0.04270059278364587}, {‘weights’: [-2.5584149848484263, 1.0036422106209202, 0.42383086467582715], ‘output’: 0.7790535202438367, ‘delta’: 0.03803132596437354}]
To make a prediction, we can use the set of weights already configured in the previous example.
Prediction
from math import exp # Calculate neuron activation for an input def activate(weights, inputs): activation = weights[-1] for i in range(len(weights)-1): activation += weights[i] * inputs[i] return activation # Transfer neuron activation def transfer(activation): return 1.0 / (1.0 + exp(-activation)) # Forward propagate input to a network output def forward_propagate(network, row): inputs = row for layer in network: new_inputs = [] for neuron in layer: activation = activate(neuron['weights'], inputs) neuron['output'] = transfer(activation) new_inputs.append(neuron['output']) inputs = new_inputs return inputs # Make a prediction with a network def predict(network, row): outputs = forward_propagate(network, row) return outputs.index(max(outputs)) # Test making predictions with the network dataset = [[2.7810836,2.550537003,0], [1.465489372,2.362125076,0], [3.396561688,4.400293529,0], [1.38807019,1.850220317,0], [3.06407232,3.005305973,0], [7.627531214,2.759262235,1], [5.332441248,2.088626775,1], [6.922596716,1.77106367,1], [8.675418651,-0.242068655,1], [7.673756466,3.508563011,1]] network = [[{'weights': [-1.482313569067226, 1.8308790073202204, 1.078381922048799]}, {'weights': [0.23244990332399884, 0.3621998343835864, 0.40289821191094327]}], [{'weights': [2.5001872433501404, 0.7887233511355132, -1.1026649757805829]}, {'weights': [-2.429350576245497, 0.8357651039198697, 1.0699217181280656]}]] for row in dataset: prediction = predict(network, row) print('Expected=%d, Got=%d' % (row[-1], prediction))
When the example executes, it prints the expected result for each record in the training dataset, which is followed by a clear prediction made by the network.
According to the results, the network achieves 100% accuracy on this small dataset.
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
3. Creating a simple model using Keras and TensorFlow.
To collect data, we will use the MetaTrader 5 package. Launch the script by importing the libraries needed to extract, convert and predict the prices. We will not consider data preparation in detail here, however please do not forget that this is a very important step for the model.
Let’s start with a brief data overview. The dataset is composed of the last 1000 EURUSD bars. This part consists of several steps:
- Importing libraries
- Connecting with MetaTrader
- Collecting data
- Converting data, adjusting the dates
- Plot data
import MetaTrader5 as mt5 from pandas import to_datetime, DataFrame import matplotlib.pyplot as plt symbol = "EURUSD" if not mt5.initialize(): print("initialize() failed") mt5.shutdown() rates = mt5.copy_rates_from_pos(symbol, mt5.TIMEFRAME_D1, 0, 1000) mt5.shutdown() rates = DataFrame(rates) rates['time'] = to_datetime(rates['time'], unit='s') rates = rates.set_index(['time']) plt.figure(figsize = (15,10)) plt.plot(rates.close) plt.show()
After running the code, visualize the closing data as a line on the chart below.
Let’s use a simple regression approach to predict the closing value of the next period.
For this example we will use a univariate approach.
Univariate time series is a data set composed of a single series of observations with a temporal ordering. It needs a model to learn from the series of past observations to predict the next value in the sequence.
The first step is to split the loaded series into a training set and a testing set. Let’s create a function that will split such a series into two parts. Splitting will be performed according to the specified percentage, for example 70% for training and 30% for testing. For validation (backtest), we have other approaches such as dividing the series into training, testing and validation. Since we are talking about financial series, we should be very careful to avoid overfitting.
The function will receive a numpy array and clipping value, and it will return two split series.
The first return value is the entire set from position 0 to the size, which represents the size of the factor, and the second series is the remaining set.
def train_test_split(values, fator): train_size = int(len(values) * fator) return values[0:train_size], values[train_size:len(values)]
Keras models can be defined as a sequence of layers.
We’ll create a sequential model and add layers, one in a time, until we are happy with our network architecture.
First of all, we need to make sure that the input layer has the correct number of input resources. This can be done by creating the first layer with the argument input_dim.
How do we know how many layers and types we need?
It is a very difficult question. There are heuristics we can use, and often the best network structure is found through trial and error experimentation. Generally, you need a network large enough to capture the structure of the problem.
In this example, we will use a fully connected single-layer network structure.
Fully connected layers are defined using the Dense class. We can specify the number of neurons or nodes in a layer as the first argument and specify the activation function using the activation argument.
We will use the rectified linear unit (ReLU) activation function in the first layer.
Before a univariate series can be predicted, it must be prepared.
The MLP model will learn using a function that maps a sequence of past observations as input into output observations. Thus, the sequence of observations must be transformed into multiple examples from which the model can learn.
Consider a univariate sequence:
[10, 20, 30, 40, 50, 60, 70, 80, 90]
The sequence can be split into several I/O patterns called samples.
In our example, we will use three time steps that are used as input and one time step that is used for output in studied prediction.
X, y
10, 20, 30 40
20, 30, 40 50
30, 40, 50 60
…
Below, we create the split_sequence() function that implement this behavior. We will also split the univariate set into several samples where each has a certain number of time steps. The output is a single time step.
We can test our function on a small set of data, like the data in the above example.
# univariate data preparation from numpy import array # split a univariate sequence into samples def split_sequence(sequence, n_steps): X, y = list(), list() for i in range(len(sequence)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the sequence if end_ix > len(sequence)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequence[i:end_ix], sequence[end_ix] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90] # choose a number of time steps n_steps = 3 # split into samples X, y = split_sequence(raw_seq, n_steps) # summarize the data for i in range(len(X)): print(X[i], y[i])
The code splits a univariate set into six samples, each having three input time steps and one output time step.
[10 20 30] 40
[20 30 40] 50
[30 40 50] 60
[40 50 60] 70
[50 60 70] 80
[60 70 80] 90
To continue, we need to split the sample into X (feature) and y (target) so that we can train the network. To do this, we will use the earlier created split_sequence() function.
X_train, y_train = split_sequence(train, 3) X_test, y_test = split_sequence(test, 3)
Now that we have prepared data samples, we can create the MLP network.
A simple MLP model has only one hidden layer of nodes (neurons) and an output layer used for prediction.
We can define the MLP for predicting univariate time series as follows.
# define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_steps)) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse')
To define the form of input data, we need to understand what the model expects to receive as input data for each sample in terms of the number of time steps.
The number of time steps as input is the number that we choose when preparing the data set as an argument for the split_sequence() function.
The input dimension of each sample is specified in the input_dim argument in the definition of the first hidden layer. Technically, the model will display each time step as a separate resource rather than separate time steps.
Usually we have multiple samples, so the model expects that the input training component will have dimensions or shape:
[samples, features]
The split_sequence() function generates X with the form [samples, characteristics] which is ready to use.
The model is trained using the efficient algorithm called Adam for the stochastic gradient descent. It is optimized using the MSE (means square error) loss function.
Having defined the model, we can train it using the dataset.
model.fit(X_train, y_train, epochs=100, verbose=2)
After training the model, we can predict the future value. The model expects the input shape to be two-dimensional [samples, characteristics], therefore we need to reshape the single input sample before making the prediction. For example, using the form [1, 3] for 1 sample and 3 time steps used as characteristics.
Let’s select the last record of the test sample X_test and after predicting we will compare it with the real value contained in the last sample y_test.
# demonstrate prediction x_input = X_test[-1] x_input = x_input.reshape((1, n_steps)) yhat = model.predict(x_input, verbose=0) print("Valor previsto: ", yhat) print("Valor real: ", y_test[-1])
4. How to integrate MQL5 and Python.
We have a few options to use the model on a trading account. One of them is to use native Python functions that open and close positions. But in this case we miss wide opportunities offered by MQL. For this reason, I’ve chosen integration between Python and the MQL environment, which will give us more autonomy in managing positions/orders.
Based on the article MetaTrader 5 and Python integration: receiving and sending data by Maxim Dmitrievsky, I have implemented this class using the Singleton pattern which will be responsible for the creation of a Socket client for communication. This pattern ensures that there is only one copy of a certain type of object because if the program uses two pointers, both referring to the same object, the pointers will point to the same object.
class CClientSocket { private: static CClientSocket* m_socket; int m_handler_socket; int m_port; string m_host; int m_time_out; CClientSocket(void); ~CClientSocket(void); public: static bool DeleteSocket(void); bool SocketSend(string payload); string SocketReceive(void); bool IsConnected(void); static CClientSocket *Socket(void); bool Config(string host, int port); bool Close(void); };
The CClienteSocke class stores the static pointer as a private member. The class has only one constructor which is private and cannot be called. Instead of constructor code, we can use the Socket method to guarantee that only one object is used.
static CClientSocket *CClientSocket::Socket(void) { if(CheckPointer(m_socket)==POINTER_INVALID) m_socket=new CClientSocket(); return m_socket; }
This method checks if the static pointer points at the CClienteSocket socket. If true it returns the reference; otherwise a new object is created and associated with the pointer, thus ensuring that this object is exclusive in our system.
To establish a connection with the server, it is necessary to initiate the connection. Here is the IsConnected method to establish a connection, after which we can start sending/receiving data.
bool CClientSocket::IsConnected(void) { ResetLastError(); bool res=true; m_handler_socket=SocketCreate(); if(m_handler_socket==INVALID_HANDLE) res= false ; if(!::SocketConnect(m_handler_socket,m_host,m_port,m_time_out)) res= false ; return res; }
After successful connection and transmission of messages, we need to close this connection. To do this, we’ll use the Close method to close the previously opened connection.
bool CClientSocket::Close(void) { bool res=false; if(SocketClose(m_handler_socket)) { res=true; m_handler_socket=INVALID_HANDLE; } return res; }
Now we need to register the server that will receive new MQL connections and send predictions to our model.
import socket class socketserver(object): def __init__(self, address, port): self.sock = socket.socket(socket.AF_INET, socket.SOCK_STREAM) self.address = address self.port = port self.sock.bind((self.address, self.port)) def socket_receive(self): self.sock.listen(1) self.conn, self.addr = self.sock.accept() self.cummdata = '' while True: data = self.conn.recv(10000) self.cummdata+=data.decode("utf-8") if not data: self.conn.close() break return self.cummdata def socket_send(self, message): self.sock.listen(1) self.conn, self.addr = self.sock.accept() self.conn.send(bytes(message, "utf-8")) def __del__(self): self.conn.close()
Our object is simple: in its constructor we receive the address and the port of our server. The socket_received method is responsible for accepting the new connection and for checking the existence of sent messages. If there are messages to be received, we run a loop until we receive all the part of the message. Then close connection with the client and exit the loop. On the other hand, the socket_send method is responsible for sending messages to our client. So, this proposed model not only allows us to send predictions to our model, but also opens up possibilities for several other things – it all depends on your creativity and needs.
Now we have the ready communication. Let’s think about two things:
- How to train the model and save it.
- How to use the trained model to make predictions.
It would be impractical and wrong to get data and train every time we want to make a prediction. For this reason, I always do some training, find the best hyperparameters and save my model for later use.
I will create a file named model_train which will contain the network training code. We will use the percentage difference between closing prices and will try to predict this difference. Please note that I only want to show how to use the model by integrating with the MQL environment, but not the model itself.
import MetaTrader5 as mt5 from numpy.lib.financial import rate from pandas import to_datetime, DataFrame from datetime import datetime, timezone from matplotlib import pyplot from sklearn.metrics import mean_squared_error from math import sqrt import numpy as np from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense from tensorflow.keras.callbacks import * symbol = "EURUSD" date_ini = datetime(2020, 1, 1, tzinfo=timezone.utc) date_end = datetime(2021, 7, 1, tzinfo=timezone.utc) period = mt5.TIMEFRAME_D1 def train_test_split(values, fator): train_size = int(len(values) * fator) return np.array(values[0:train_size]), np.array(values[train_size:len(values)]) # split a univariate sequence into samples def split_sequence(sequence, n_steps): X, y = list(), list() for i in range(len(sequence)): end_ix = i + n_steps if end_ix > len(sequence)-1: break seq_x, seq_y = sequence[i:end_ix], sequence[end_ix] X.append(seq_x) y.append(seq_y) return np.array(X), np.array(y) if not mt5.initialize(): print("initialize() failed") mt5.shutdown() raise Exception("Error Getting Data") rates = mt5.copy_rates_range(symbol, period, date_ini, date_end) mt5.shutdown() rates = DataFrame(rates) if rates.empty: raise Exception("Error Getting Data") rates['time'] = to_datetime(rates['time'], unit='s') rates.set_index(['time'], inplace=True) rates = rates.close.pct_change(1) rates = rates.dropna() X, y = train_test_split(rates, 0.70) X = X.reshape(X.shape[0]) y = y.reshape(y.shape[0]) train, test = train_test_split(X, 0.7) n_steps = 60 verbose = 1 epochs = 50 X_train, y_train = split_sequence(train, n_steps) X_test, y_test = split_sequence(test, n_steps) X_val, y_val = split_sequence(y, n_steps) # define model model = Sequential() model.add(Dense(200, activation='relu', input_dim=n_steps)) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse') history = model.fit(X_train ,y_train ,epochs=epochs ,verbose=verbose ,validation_data=(X_test, y_test)) model.save(r'C:\YOUR_PATH\MQL5\Experts\YOUR_PATH\model_train_'+symbol+'.h5') pyplot.title('Loss') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() history = list() yhat = list() for i in range(0, len(X_val)): pred = X_val[i] pred = pred.reshape(( 1 , n_steps)) history.append(y_val[i]) yhat.append(model.predict(pred).flatten()[0]) pyplot.figure(figsize=(10, 5)) pyplot.plot(history,"*") pyplot.plot(yhat,"+") pyplot.plot(history, label='real') pyplot.plot(yhat, label='prediction') pyplot.ylabel('Price Close', size=10) pyplot.xlabel('time', size=10) pyplot.legend(fontsize= 10 ) pyplot.show() rmse = sqrt(mean_squared_error(history, yhat)) mse = mean_squared_error(history, yhat) print('Test RMSE: %.3f' % rmse) print('Test MSE: %.3f' % mse)
We now have a trained model, which is saved in the folder with the .h5 extension. We can use this model for predictions. Now let’s create an object that will instantiate this model to be used for connection.
from tensorflow.keras.models import * class Model(object): def __init__(self, n_steps:int, symbol:str, period:int) -> None: super().__init__() self.n_steps = n_steps self.model = load_model(r'C:\YOUR_PATH\MQL5\Experts\YOUR_PATH\model_train_'+symbol+'.h5') def predict(self, data): return(self.model.predict(data.reshape((1, self.n_steps))).flatten()[0])
The object is simple: its constructor creates an instance of the attribute called model, which will contain the saved model. The predict model is responsible for making the prediction.
Now we need the main method that will work and interact with clients, receiving functions and sending predictions
import ast import pandas as pd from model import Model from server_socket import socketserver host = 'localhost' port = 9091 n_steps = 60 TIMEFRAME = 24 | 0x4000 model = Model(n_steps, "EURUSD", TIMEFRAME) if __name__ == "__main__": serv = socketserver(host, port) while True: print("<<--Waiting Prices to Predict-->>") rates = pd.DataFrame(ast.literal_eval(serv.socket_receive())) rates = rates.rates.pct_change(1) rates.dropna(inplace=True) rates = rates.values.reshape((1, n_steps)) serv.socket_send(str(model.predict(rates).flatten()[0]))
On the MQL client side, we need to create a robot that will collect data and send it to our server, from which it will receive predictions. Since our model was trained with the data from closed candlesticks, we need to add a check that data will only be collected and sent after a candlestick closes. We should have the complete data to predict the difference for the closing of the current bar that has just started. We will use a function that checks the emergence of a new bar.
bool NewBar(void) { datetime time[]; if(CopyTime(Symbol(), Period(), 0, 1, time) < 1) return false; if(time[0] == m_last_time) return false; return bool(m_last_time = time[0]); }
The m_last_time variable is declared in the global scope. It will store the bar opening date and time. So, we will check if the ‘time’ variable differs from m_last_time: if true, then a new bar has started. In this case, the m_last_time should be replaced with ‘time’.
The EA should not open a new position if there is already an open position. Therefore, check the existence of open positions using the CheckPosition method which sets true or false for buy and sell variables declared in the global scope.
void CheckPosition(void) { buy = false; sell = false; if(PositionSelect(Symbol())) { if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_BUY&&PositionGetInteger(POSITION_MAGIC) == InpMagicEA) { buy = true; sell = false; } if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_SELL&&PositionGetInteger(POSITION_MAGIC) == InpMagicEA) { sell = true; buy = false; } } }
When a new bar appears, check if there are any open positions. If there is an open position, wait for it to be closed. If there is no open position, initiate the connection process by calling the IsConnected method of the CClienteSocket class.
if(NewBar()) { if(!Socket.IsConnected()) Print("Error : ", GetLastError(), " Line: ", __LINE__); ... }
If true is returned, which means we can establish connection with the server, collect data and send it back.
string payload = "{'rates':["; for(int i=InpSteps; i>=0; i--) { if(i>=1) payload += string(iClose(Symbol(), Period(), i))+","; else payload += string(iClose(Symbol(), Period(), i))+"]}"; }
I decided to send the data in the format of {‘rates’:[1,2,3,4]} — this way we convert them to a pandas dataframe and there is no need to waste time on data conversions.
Once the data has been collected, send them and wait for a prediction, based on which a decision can be made. I will use a moving average to check the price direction. Depending on the price direction and the value of the prediction, we will buy or sell.
void OnTick(void) { .... bool send = Socket.SocketSend(payload); if(send) { if(!Socket.IsConnected()) Print("Error : ", GetLastError(), " Line: ", __LINE__); double yhat = StringToDouble(Socket.SocketReceive()); Print("Value of Prediction: ", yhat); if(CopyBuffer(handle, 0, 0, 4, m_fast_ma)==-1) Print("Error in CopyBuffer"); if(m_fast_ma[1]>m_fast_ma[2]&&m_fast_ma[2]>m_fast_ma[3]) { if((iClose(Symbol(), Period(), 2)>iOpen(Symbol(), Period(), 2)&&iClose(Symbol(), Period(), 1)>iOpen(Symbol(), Period(), 1))&&yhat<0) { m_trade.Sell(mim_vol); } } if(m_fast_ma[1]<m_fast_ma[2]&&m_fast_ma[2]<m_fast_ma[3]) { if((iClose(Symbol(), Period(), 2)<iOpen(Symbol(), Period(), 2)&&iClose(Symbol(), Period(), 1)<iOpen(Symbol(), Period(), 1))&&yhat>0) { m_trade.Buy(mim_vol); } } } Socket.Close(); } }
The last step is to close the previously established connection and wait for the emergence of a new bar. When a new bar opens, start the process of sending the data and receiving the prediction.
This architecture proves to be very useful and to have low latency. In some personal projects I use this architecture in trading accounts as it allows me to enjoy the full power of MQL and along with the extensive resources available in Python for Machine Learning.
What’s next?
In the next article, I want to develop a more flexible architecture that will allow the use of models in the strategy tester.
Conclusion
I hope this is a useful small tutorial on how to use and develop various Python models and how to integrate them with the MQL environment.
In this article we:
- Set up the Python development environment.
- Implemented the perceptron neuron and the MLP network in Python.
- Prepared univariate data for learning a simple network.
- Set up the architecture of communication between Python and MQL.
Further ideas
This section provides some additional ideas which can help you in expanding this tutorial.
- Input size. Explore the number of days used for model input, for example 21 days, 30 days.
- Model tuning. Study various structures and hyperparameters to get the average model performance.
- Data scaling. Find out if you can use data size, such as standardization and normalization, to improve model performance.
- Learning diagnostics. Use diagnostics such as learning curves for loss of learning and validation; use root mean square error to help tune the structure and hyperparameters of the model.
If you explore further these extension opportunities, please share your ideas.